Was macht ein Quadrat eigentlich zu einem Quadrat? Die Antwort liegt in seinen Abmessungen.
Die charakteristische Eigenschaft eines Quadrats ist die Gleichheit all seiner Seiten. Diese Seitenlänge ist die grundlegende Dimension, aus der sich alle anderen Eigenschaften ableiten lassen. Das Verständnis dieser Dimensionen ist der Schlüssel zur Berechnung von Flächeninhalt, Umfang und zur Anwendung des Quadrats in verschiedenen Bereichen.
Von der Geometrie bis zur Architektur, von der Kunst bis zum Alltag – das Quadrat und seine Abmessungen spielen eine wichtige Rolle. Dieser Artikel beleuchtet die verschiedenen Aspekte der Quadrat-Dimensionen und bietet ein umfassendes Verständnis dieses fundamentalen geometrischen Gebildes.
Wir betrachten nicht nur die mathematischen Grundlagen, sondern auch die praktische Bedeutung der Quadrat-Dimensionen. Von der Berechnung der Fläche eines quadratischen Raumes bis zur Konstruktion eines perfekten Quadrats – hier finden Sie alle wichtigen Informationen.
Begeben wir uns also auf eine Entdeckungsreise in die Welt der Quadrate und ihrer Maße. Von den grundlegenden Definitionen bis zu praktischen Anwendungen werden wir die verschiedenen Facetten dieses einfachen, aber faszinierenden geometrischen Objekts erkunden.
Die Geschichte des Quadrats reicht weit zurück. Schon in der Antike erkannten Menschen die besondere Bedeutung dieser Form. In der griechischen Mathematik spielte das Quadrat eine zentrale Rolle, beispielsweise bei der Untersuchung von Flächeninhalten und der Entdeckung irrationaler Zahlen wie der Quadratwurzel aus 2. Die Abmessungen eines Quadrats – seine Seitenlänge – wurden frühzeitig als Grundlage für Berechnungen verwendet.
Die Seitenlänge eines Quadrats bestimmt dessen Größe und alle weiteren abgeleiteten Maße. Der Flächeninhalt, also die Größe der Fläche innerhalb des Quadrats, wird berechnet, indem die Seitenlänge mit sich selbst multipliziert wird (Seitenlänge * Seitenlänge). Der Umfang, die Gesamtlänge aller Seiten, ergibt sich aus der vierfachen Seitenlänge (4 * Seitenlänge). Ein Quadrat mit der Seitenlänge 5 cm hat demnach einen Flächeninhalt von 25 cm² und einen Umfang von 20 cm.
Ein Vorteil der klaren Dimensionalität des Quadrats ist die einfache Berechnung von Flächeninhalt und Umfang. Dies ist besonders im Bauwesen und in der Architektur von Bedeutung. Ein weiterer Vorteil ist die ästhetische Wirkung des Quadrats, die in der Kunst und im Design geschätzt wird. Die Symmetrie und Ausgewogenheit des Quadrats verleihen ihm eine besondere Harmonie.
Vor- und Nachteile eines Quadrats
| Vorteile | Nachteile |
|---|---|
| Einfache Berechnungen | Eingeschränkte Formgebung im Vergleich zu anderen Polygonen |
| Symmetrie und Ästhetik | Weniger flexibel als ein Rechteck |
| Stabilität (in der Konstruktion) |
Häufig gestellte Fragen:
1. Was ist ein Quadrat? Antwort: Ein Viereck mit gleich langen Seiten und rechten Winkeln.
2. Wie berechnet man den Flächeninhalt? Antwort: Seitenlänge * Seitenlänge.
3. Wie berechnet man den Umfang? Antwort: 4 * Seitenlänge.
4. Was ist die Diagonale eines Quadrats? Antwort: Die Verbindungslinie zwischen zwei gegenüberliegenden Ecken.
5. Wie berechnet man die Diagonale? Antwort: Seitenlänge * Wurzel(2).
6. Wo werden Quadrate in der Praxis verwendet? Antwort: Architektur, Design, Kunst, Mathematik.
7. Was ist der Unterschied zwischen einem Quadrat und einem Rechteck? Antwort: Ein Quadrat ist ein spezielles Rechteck mit gleich langen Seiten.
8. Was ist ein Einheitsquadrat? Antwort: Ein Quadrat mit der Seitenlänge 1.
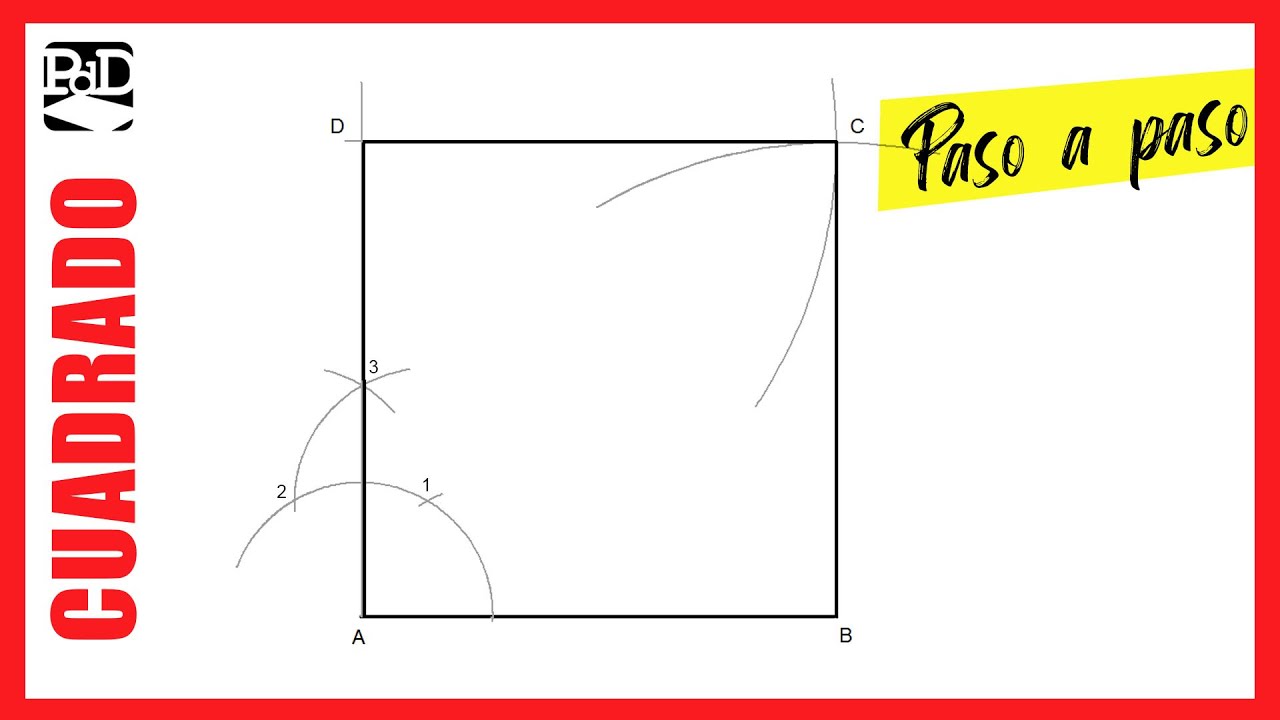
Tipps und Tricks: Um ein Quadrat zu konstruieren, benötigt man lediglich ein Lineal und einen Winkelmesser. Man zeichnet zuerst eine Strecke mit der gewünschten Seitenlänge und konstruiert dann an beiden Endpunkten rechte Winkel. Anschließend zeichnet man zwei weitere Strecken mit der gleichen Länge, die die Endpunkte der ersten Strecke verbinden.
Zusammenfassend lässt sich sagen, dass das Verständnis der Abmessungen eines Quadrats – insbesondere der Seitenlänge – grundlegend für die Berechnung seines Flächeninhalts und Umfangs ist. Das Quadrat findet aufgrund seiner einfachen Geometrie und ästhetischen Eigenschaften vielfältige Anwendungen in verschiedenen Bereichen, von der Mathematik und Architektur bis hin zur Kunst und dem alltäglichen Leben. Die klaren Dimensionen des Quadrats ermöglichen einfache Berechnungen und bieten eine solide Grundlage für komplexere geometrische Konstruktionen. Erforschen Sie die Welt der Quadrate und entdecken Sie die faszinierenden Möglichkeiten, die diese einfache Form bietet.
Coole geburtstagstexte fur frauen zum 30
Der ursprung des dunklen ritters batman entstehungsgeschichte
Blitzschnelle kartoffel power fur die mittagspause