Heb je je ooit afgevraagd hoe sterk de relatie is tussen twee variabelen? Stel, je wilt weten of er een verband is tussen de hoeveelheid ijsjes die verkocht worden en de temperatuur. Of misschien wil je onderzoeken of er een correlatie is tussen studie-uren en cijfers. De product-moment correlatiecoëfficiënt (ook wel Pearson correlatie genoemd) en de bijbehorende r-tabel bieden hierbij uitkomst. Ze geven inzicht in de sterkte en richting van lineaire verbanden tussen twee variabelen.
De product-moment correlatiecoëfficiënt, vaak aangeduid als 'r', is een statistische maat die de lineaire samenhang tussen twee continue variabelen kwantificeert. De waarde van 'r' varieert van -1 tot +1. Een 'r' van +1 duidt op een perfecte positieve correlatie, wat betekent dat wanneer de ene variabele toeneemt, de andere variabele ook proportioneel toeneemt. Een 'r' van -1 duidt op een perfecte negatieve correlatie, wat betekent dat wanneer de ene variabele toeneemt, de andere variabele proportioneel afneemt. Een 'r' van 0 geeft aan dat er geen lineair verband is tussen de variabelen.
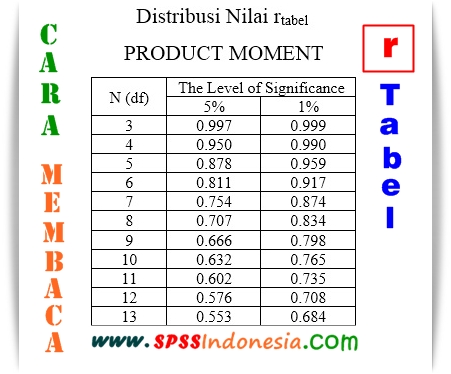
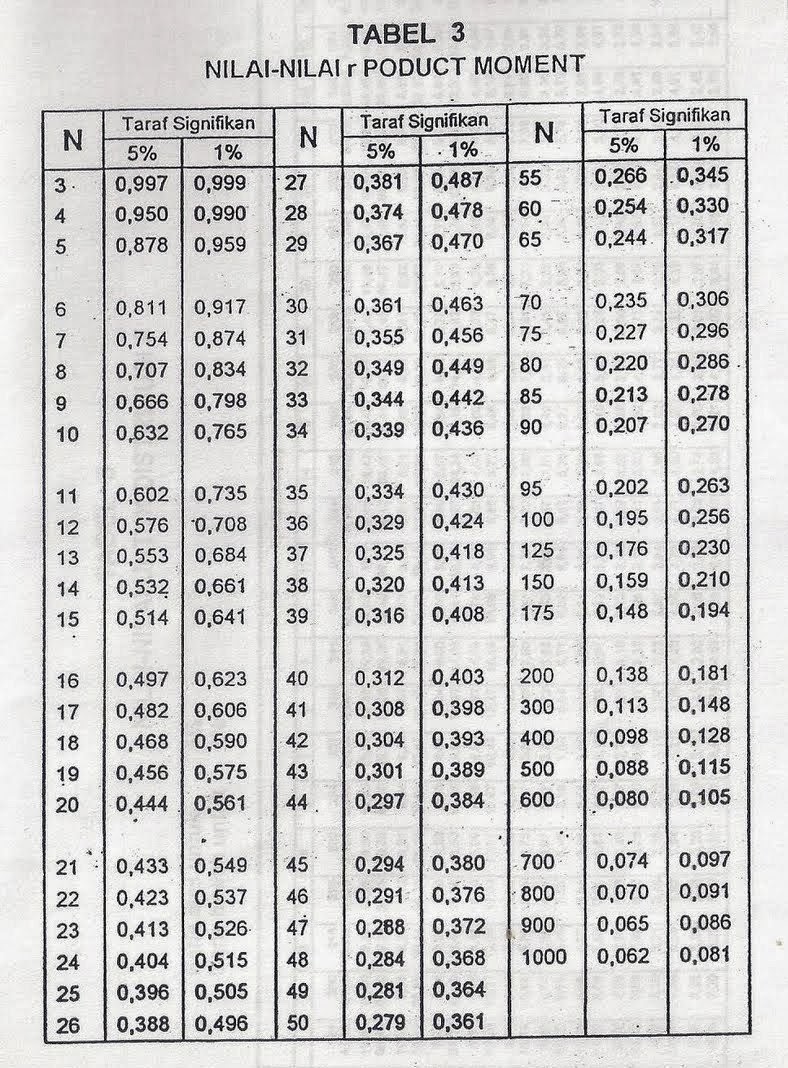
Om de significantie van de berekende 'r' te bepalen, gebruiken we de r-tabel (ook wel de kritieke waarden tabel voor de Pearson correlatie genoemd). Deze tabel geeft de kritieke waarden van 'r' voor verschillende steekproefgroottes en significantieniveaus (alfa). Door de berekende 'r' te vergelijken met de kritieke waarde in de tabel, kunnen we bepalen of de correlatie statistisch significant is. Een statistisch significante correlatie betekent dat het onwaarschijnlijk is dat de gevonden correlatie op toeval berust.
Het concept van correlatie en de r-tabel zijn ontwikkeld door Karl Pearson aan het begin van de 20e eeuw en spelen een cruciale rol in diverse wetenschappelijke disciplines, van psychologie en sociologie tot economie en biologie. Ze worden gebruikt om relaties tussen variabelen te onderzoeken en hypothesen te toetsen.
Een belangrijk punt om te onthouden is dat correlatie niet gelijk staat aan causaliteit. Een significante correlatie tussen twee variabelen betekent niet noodzakelijkerwijs dat de ene variabele de andere veroorzaakt. Er kunnen andere factoren in het spel zijn die de relatie tussen de variabelen beïnvloeden. Verder is de product-moment correlatiecoëfficiënt alleen geschikt voor het meten van lineaire verbanden. Niet-lineaire verbanden kunnen niet adequaat worden weergegeven met 'r'.
Een voorbeeld: Stel je voor dat je de correlatie wilt bepalen tussen de temperatuur en het aantal verkochte ijsjes. Je verzamelt data over een periode van 30 dagen en berekent een 'r' van 0.85. Dit suggereert een sterke positieve correlatie. Door deze 'r' te vergelijken met de kritieke waarde in de r-tabel voor een steekproefgrootte van 30 en een alfa van 0.05, kun je vaststellen of deze correlatie statistisch significant is.
Voor- en Nadelen van de Product-Moment Correlatiecoëfficiënt
| Voordelen | Nadelen |
|---|---|
| Eenvoudig te berekenen en interpreteren | Gevoelig voor outliers |
| Veelgebruikte en geaccepteerde statistische maat | Alleen geschikt voor lineaire verbanden |
| Helpt bij het identificeren van relaties tussen variabelen | Correlatie is niet gelijk aan causaliteit |
Veelgestelde Vragen:
1. Wat is de r-tabel? Antwoord: De r-tabel geeft kritieke waarden voor de Pearson correlatie.
2. Wat betekent een negatieve r-waarde? Antwoord: Een negatieve r-waarde duidt op een negatieve correlatie.
3. Wat is een significantieniveau? Antwoord: Het significantieniveau (alfa) bepaalt de kans op een Type I fout.
4. Kan ik de r-tabel online vinden? Antwoord: Ja, er zijn veel online bronnen beschikbaar.
5. Wat is het verschil tussen correlatie en causaliteit? Antwoord: Correlatie impliceert geen causaliteit.
6. Wat is de product-moment correlatiecoëfficiënt? Antwoord: Een maat voor de lineaire samenhang tussen twee variabelen.
7. Hoe interpreteer ik een r-waarde van 0? Antwoord: Geen lineair verband.
8. Wat is een sterke correlatie? Antwoord: Een r-waarde dicht bij +1 of -1.
De product-moment correlatiecoëfficiënt en de r-tabel zijn krachtige instrumenten voor het analyseren van relaties tussen variabelen. Hoewel correlatie geen causaliteit impliceert, biedt 'r' waardevolle inzichten in de sterkte en richting van lineaire verbanden. Door de 'r' te vergelijken met de kritieke waarden in de r-tabel, kunnen we de significantie van de correlatie beoordelen en gefundeerde conclusies trekken over de relatie tussen variabelen. Het begrijpen van deze concepten is essentieel voor iedereen die data analyseert en interpretaties wil maken over de wereld om ons heen. Door kritisch na te denken over de interpretatie van de resultaten en rekening te houden met de beperkingen van de methode, kunnen we waardevolle informatie halen uit correlatiestudies. Blijf leren en ontdekken hoe statistiek je kan helpen bij het begrijpen van complexe verbanden in data!
Die ene song dont lose my number onthouden
Moderna vaccin effectiviteit alles wat je moet weten
Op zoek naar je droomauto ontdek white cottage car centre mirfield
