Stel je voor: je staat aan de voet van een majestueuze berg, de top gehuld in mysterieuze mist. Je wilt de steilheid van de helling bepalen, de mathematische essentie van deze imposante reus. Hoe pak je dat aan? Het antwoord ligt in het hellingsgetal. Deze wiskundige waarde onthult de steilheid van een lijn, een essentieel concept in diverse vakgebieden, van architectuur tot natuurkunde.
Het hellingsgetal, ook wel de richtingscoëfficiënt genoemd, kwantificeert de verandering in de verticale richting ten opzichte van de horizontale richting. Het geeft ons inzicht in hoe snel een lijn stijgt of daalt. Beheersing van dit concept opent deuren naar een dieper begrip van lineaire relaties en hun toepassingen in de echte wereld.
De berekening van het hellingsgetal is relatief eenvoudig, maar de implicaties ervan zijn verreikend. Van het ontwerpen van veilige wegen tot het voorspellen van financiële trends, het hellingsgetal speelt een cruciale rol. In deze gids duiken we diep in de wereld van het hellingsgetal, van de basisformule tot de meest complexe toepassingen.
Of je nu een student bent die worstelt met wiskunde, een professional die zijn kennis wil opfrissen, of gewoon een nieuwsgierige geest die de geheimen van de helling wil ontsluieren, deze gids biedt je de tools en inzichten die je nodig hebt.
Bereid je voor op een fascinerende reis door de wereld van het hellingsgetal, waar wiskunde en de echte wereld samenkomen om de mysteries van de helling te ontrafelen.
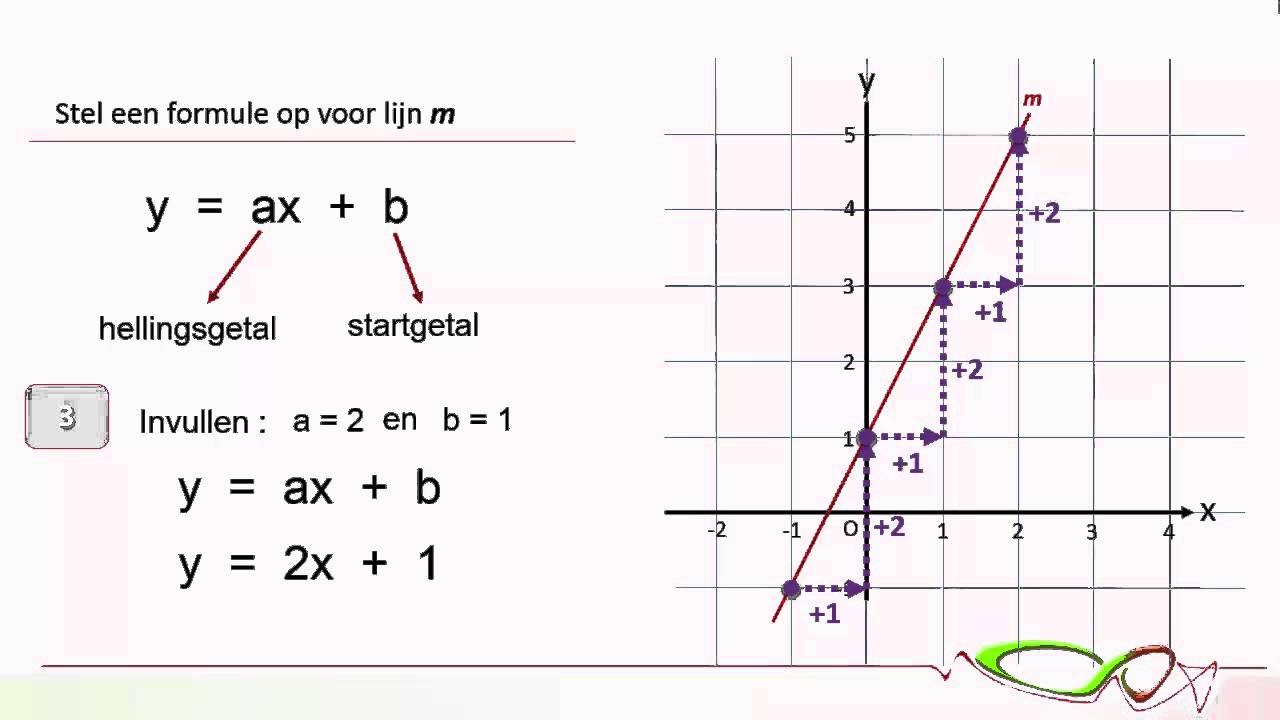
De formule voor het hellingsgetal (m) is: m = (y2 - y1) / (x2 - x1), waarbij (x1, y1) en (x2, y2) twee punten op de lijn zijn. Deze formule, afgeleid van de principes van de analytische meetkunde, legt de kern vast van de lineaire relatie tussen twee variabelen.
Een eenvoudig voorbeeld: Stel je een lijn voor die door de punten (1, 2) en (4, 8) gaat. Het hellingsgetal is dan (8 - 2) / (4 - 1) = 6 / 3 = 2. Dit betekent dat voor elke eenheid die de lijn horizontaal beweegt, deze twee eenheden verticaal stijgt.
Voordelen van het begrijpen van het hellingsgetal zijn: het voorspellen van trends, het analyseren van data en het oplossen van wiskundige problemen. Het hellingsgetal is essentieel voor het begrijpen van lineaire functies.
Stap-voor-stap handleiding: 1. Identificeer twee punten op de lijn. 2. Pas de formule m = (y2 - y1) / (x2 - x1) toe. 3. Interpreteer het resultaat.
Voor- en Nadelen van Hellingsgetal Berekenen
Hoewel het concept van het hellingsgetal krachtig is, zijn er nuances waarmee rekening moet worden gehouden:
Veelgestelde vragen:
1. Wat is een hellingsgetal? Antwoord: De mate van steilheid van een lijn.
2. Hoe bereken je de richtingscoëfficiënt? Antwoord: Met de formule (y2 - y1) / (x2 - x1).
3. Wat betekent een negatief hellingsgetal? Antwoord: Een dalende lijn.
4. Wat betekent een hellingsgetal van nul? Antwoord: Een horizontale lijn.
5. Wat is een oneindig hellingsgetal? Antwoord: Een verticale lijn.
6. Hoe gebruik je het hellingsgetal in de praktijk? Antwoord: Bijvoorbeeld in de bouw, natuurkunde en economie.
7. Waar kan ik meer informatie vinden over het hellingsgetal? Antwoord: Op wiskunde websites en in leerboeken.
8. Wat is het verschil tussen hellingsgetal en richtingscoëfficiënt? Antwoord: Het zijn synoniemen.
Tips en trucs: Let op de volgorde van de coördinaten in de formule.
Conclusie: Het hellingsgetal is een fundamenteel concept in de wiskunde met brede toepassingen in diverse disciplines. Van het ontwerpen van infrastructuur tot het analyseren van financiële data, het begrijpen van het hellingsgetal opent deuren naar een dieper begrip van de wereld om ons heen. Door de eenvoudige formule toe te passen en de interpretatie ervan te beheersen, kunnen we de geheimen van de helling ontsluieren en de kracht van lineaire relaties benutten. Begin vandaag nog met het verkennen van de fascinerende wereld van het hellingsgetal en ontdek de talloze mogelijkheden die het biedt. De steilheid van je leercurve zal ongetwijfeld een positief hellingsgetal hebben!
De magie van een dierenknuffel waarom die omarming zo belangrijk is
Im namen des herrn film ontdekken
Tijdmeting toetsen de klok rond succesvol
